Sekelmaan kan wel driehoekig wees

Maar 'n sirkel kan nie vierkantig gemaak word nie

Baie van ons het al gehoor van die wiskundige cliché dat jy nie ’n sirkel vierkantig kan maak nie. Die idioom word alledaags gebruik om te bedoel dat ’n mens nie bloed uit ’n klip kan tap nie, met die bedoeling dat iets wat eenvoudig onmoontlik is, nie gepoog moet word nie.

Maar daar is eintlik ’n wiskundige bewys daarvoor, wat daarop neerkom dat die eienskappe van π – die verhouding tussen ’n sirkel se omtrek en sy deursnee – transendentaal is (m.a.w. die verhouding kan nie as ’n polinoom geskryf word nie).

Daar is wel ’n ander soortgelyke bewys wat waar is, en dit is dat ’n mens ’n sekelmaan wel driehoekig kan maak. Die wiskundige bewys is eerste reg gekry deur Hippokrates van Chios, wat nie verwar moet word met Hippokrates van Kos (die vader van medisyne) nie. Ek het op die meetkundige bewys afgekom toe ek Maurice Kline se boeke oor die geskiedenis van wiskundige denke begin lees het. Ek beveel dit vir enige iemand aan wat in wiskunde belangstel.

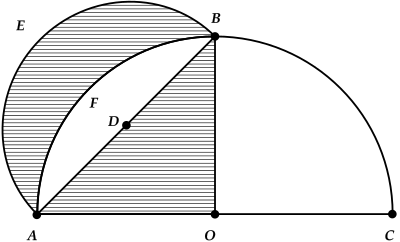
Beskou die volgende figuur.

Die figuur het die volgende eienskappe.

• OAB is beide ‘n eweredige en reghoekige driehoek, met sye OA = OB.

• Die lyn OA is ook die straal van die halwe sirkel ABCO.

• D is die punt wat die lyn AB, in twee gelyke lyne AD en AB verdeel.

• Die sirkel met die maan is ‘n halwe sirkel met ‘n straal DA.

Volgens Pythagoras se stelling het die reghoekige driehoek OAB se sye die volgende verhouding.

AB² = OA² + OB²

Maar omdat die driehoek ook eweredig is, is OA = OB,

∴ AB² = 2OA² (1)

Omdat D, die lyn AB in twee verdeel, is

AB = 2DA

∴AB² = 4DA² (2)

Vervang (1) in (2)

2OA² = 4DA²

Vermenigvuldig beide kante met π en deel met hulle faktore.

∴πOA²/4 = πDA²/2

Die term aan die linkerkant is gelykstaande aan die oppervlakke van die kwart sirkel OAFB.

Die term aan die regterkant is gelykstaande aan die oppervlak van die halwe sirkel met die sekelmaan. M.a.w. dit is die bewys dat die oppervlakte van die halwe sirkel met die maan gelykstaande is aan die kwart sirkel OAFB.

Trek nou die area ADBF af van beide oppervlaktes af en dan is wat oorbly die bewyse dat die oppervlakte van die driehoek OAB gelykstaande is aan die oppervlakte van die maan.

Dus kan jy wel die sekelmaan driehoekig maak.