The UK's electricity mix

The Wind and Natural Gas Synergy

It’s Friday, and before leaving the office, I thought I’d share a brief write-up connecting energy and mathematics.

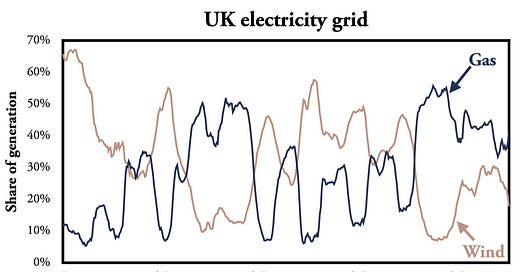
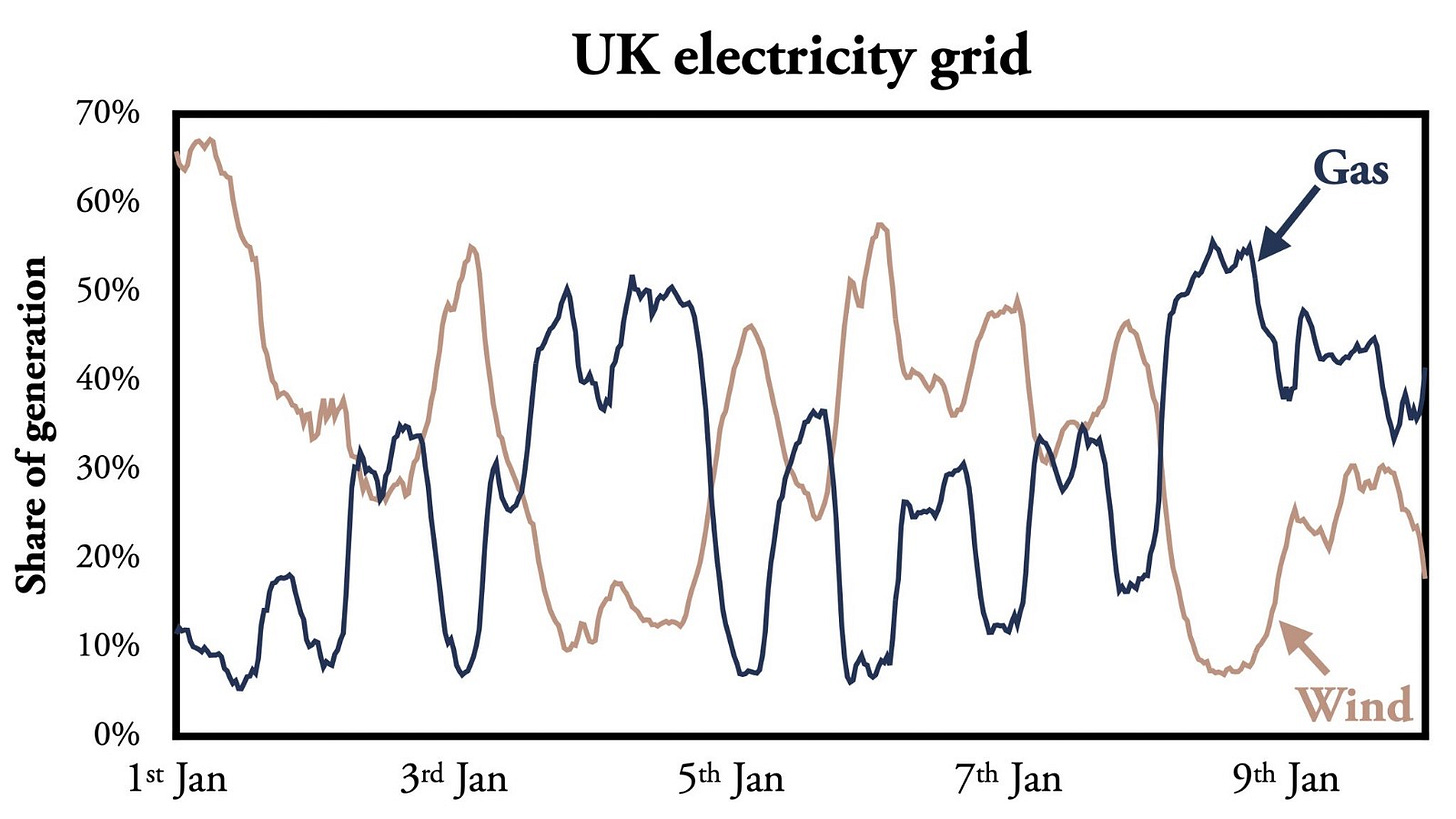
The UK’s electricity mix highlights the interdependence between natural gas and wind energy. Consequently, anyone promoting wind energy must acknowledge its inherent dependency on natural gas. The reason for this is straightforward: as I’ve explained multiple times on this blog, highly variable energy generation requires dispatchable energy sources to remain on standby. In engineering terms, this means that when the wind doesn’t blow, and the sun doesn’t shine, the system must have a reliable supply, such as natural gas.

Wind and natural gas therefore have a phase relationship that can be modeled mathematically using sine and cosine waves, as well as Euler’s identity. These techniques were pioneered by Joseph Fourier while analyzing the heat equation.

Lord Kelvin famously referred to Fourier’s work as a “great mathematical poem.