You can make the Cressent Moon triangular
Even though you cannot square the circle
Many of us have heard the mathematical cliché that you cannot circle a square. This idiom is commonly used to mean that you cannot draw blood from a stone, implying that something that is simply impossible should not be attempted.
However, there is actually a mathematical proof for this, which comes down to the fact that the properties of π – the ratio between a circle's circumference and its diameter – are transcendental (i.e., the ratio cannot be written as a polynomial).
There is, however, another similar proof that is true, and that is that you can indeed make a crescent moon triangular. The mathematical proof was first established by Hippocrates of Chios, who should not be confused with Hippocrates of Kos (the father of medicine). I came across the geometric proof when I began reading Morris Kline's books on the history of mathematical thought. I recommend it to anyone interested in the topic.
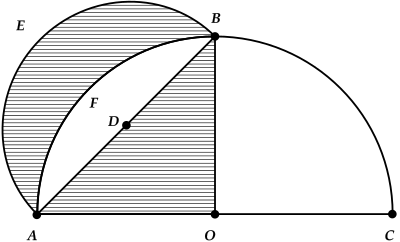
Consider the following figure.
The figure has the following properties:
OAB is both an isosceles and a right triangle, with sides OA = OB.
The line OA is also the radius of the semicircle ABCO.
D is the point that divides line AB into two equal parts, AD and DB.
The circle with the crescent is a semicircle with radius DA.
According to Pythagoras' theorem, the sides of the right triangle OAB have the following relationship:
AB² = OA² + OB²
But because the triangle is also isosceles, OA = OB,
∴ AB² = 2OA² (1)
Since D divides line AB into two equal parts, we have:
AB = 2DA
∴ AB² = 4DA² (2)
Substitute (1) into (2):
2OA² = 4DA²
Multiply both sides by π and cross divide their coefficients.
∴ πOA²/4 = πDA²/2
The term on the left side is equivalent to the area of the quarter circle OAFB.
The term on the right side is equivalent to the area of the semicircle with the crescent.
In other words, this is the proof that the area of the semicircle with the crescent is equal to the quarter circle OAFB.
Now subtract the area ADBF that is common to both surfaces, and what remains is the proof that the area of triangle OAB is equal to the area of the crescent.
Thus, you can indeed make the crescent moon triangular.