Following my last article regarding the Pythagorean Theorem, one reader suggested that real mathematics begins when one seriously considers the possibility that one of the legs of a right triangle is longer than the hypotenuse. I agree that serious mathematics begins when one goes outside of the application of real numbers and euclidean geometry in particular, but I would like to explore why this idea can also lead us on the wrong path.
I am married to a mathematician and believe me, they constantly lecture engineers and scientists for lacking rigor when blindly applying formulae! If one extends the application of the Pythagorean theorem to other fields of mathematics, mathematicians start raising eyebrows!
Let’s revisit what the Pythagorean Theorem suggests using the graph below:
and the familiar expression:
c² = b² + a²
c is the hypotenuse, and a and b are the legs of a right handed triangle.
It’s worth noting that the theorem is actually defined in euclidean space and notably Euclid's Fifth Postulate which states:
If a straight line intersects two other straight lines, and the sum of the interior angles on the same side of the intersected lines is less than 180°, then the two lines, if extended infinitely, will meet on that side.
For the laymen, Parallel lines never meet, and they are equidistant from each other at all points.
In euclidean geometry (geometry on a flat plane), the hypotenuse is defined as the side opposite the 90° angle (also known as the right angle) in the triangle. Because the sum of the internal angles of a triangle in a flat plane is always 180°, the right angle (90°) ensures that no other angle in the triangle can be greater than 90°. Given that in any triangle the longest length is always opposite the largest angle, the hypotenuse is always the longest side.
The Hypotenuse in Complex Number Contexts
However, what happens if we expand the domain of a², b², and c² to include complex numbers?
Consider the following possibility:
b² = −1, a² = 1
This leads to:
c² = 0
In ordinary Euclidean geometry, this would imply that such a triangle doesn’t exist. But if we entertain the idea of extending our discussion to complex numbers, we can look at the square roots:
a = √(1) = 1
b = √(−1) = i
c = 0
But can we conclude from the above that c > b or c < a?
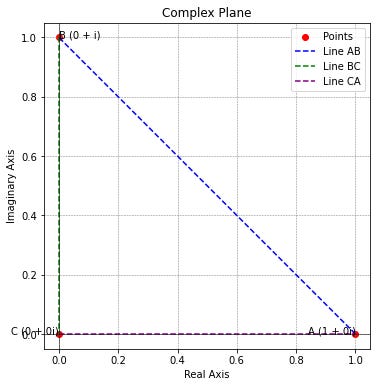
At this point, we need to recognize an important fact: complex numbers are fundamentally different from real numbers. They are represented as points in a two-dimensional plane (the complex plane), where a is on the real axis, b is on the imaginary axis, and c is at the origin.
They are not lengths and they take the general form:
z = a + ib
Magnitudes of Complex Numbers
The magnitude (or absolute value) of a complex number is given by the formula:
∣z∣=√(a² + b²) (notice that i is not part of the definition)
For our values of a, b, and c, we can compute the magnitudes as follows:
∣a∣=√(1² + 0²) =1
∣b∣=√(0² + 1²) =1
∣c∣=√(0² + 0²) = 0
Thus, both a and b have magnitudes of 1, and c has a magnitude of 0.
The distance AB on the above graph however is:
AB² = ∣a∣² + ∣b∣² = 2, which is the same answer that we would get in euclidean space from the Pythagorean theorem.
Magnitudes are real numbers, so they can be compared directly. The magnitudes ∣a∣ and ∣b∣ are equal, but it’s important to note that complex numbers themselves (like a=1 = and b=i ) cannot be compared using inequalities (terms such as greater > than or less than <), because the complex number set is not inherently ordered.
Inequalities are meaningful only within an ordered set like the real numbers.
0 > i and 0 < 1 has no meaning in the complex set, because the set is not ordered.
Only their magnitudes may be compared.
Non-Euclidean Geometry and the Hypotenuse
While the Pythagorean Theorem holds true in Euclidean geometry, we can extend the discussion to non-Euclidean geometries, such as spherical and hyperbolic geometry. These geometries differ from Euclidean geometry in that the sum of the angles in a triangle does not necessarily equal 180°.
In spherical geometry, for example, the sum of the angles of a triangle is always greater than 180°, and due to the curvature of space, the "hypotenuse" can actually be shorter than one of the legs. This happens because the geometry of the space itself changes the fundamental relationships between the sides of triangles. Similarly, in hyperbolic geometry, the sum of the angles of a triangle is less than 180°, and again, the "hypotenuse" can be shorter than the legs.
The hypotenuse can indeed be shorter than one of the legs due to the curvature of the space. The example below shows a triangle on a sphere. But the key fact remains that lines on a sphere are not actually straight lines, they are curves known as arcs .
Therefore one can say that c < b.
However, calling this the Pythagorean Theorem is also a bit of a stretch, because the definition of lines and angles within this space is different, because Euclid’s 5th postulate is violated. Two parallel lines cross, because for example all longitudes cross at the North and South Poles.
Conclusion
The Pythagorean Theorem is a cornerstone of Euclidean geometry, but when we consider extending our domain to complex numbers, we encounter the limitations of trying to apply geometric intuition. Complex numbers do not allow for direct comparisons using inequalities because they form an unordered set. However, their magnitudes can still be compared, and this gives us a way to measure "length" in the complex plane.
Finally, the idea that the hypotenuse could be shorter than one of the legs is not a result of complex analysis but rather arises from non-Euclidean geometries like spherical and hyperbolic geometry, where the space itself is curved, as is shown in the above example.
You will notice that the angles of the triangle on the sphere do not add up to 180°. This is a fundamental property of spherical geometry. In contrast, Euclidean geometry (on a flat plane) holds that the angles of a triangle always sum to exactly 180°.
However, if we define the hypotenuse as opposite the right angle (in this case, the angle at the North Pole), then it’s possible for one leg of the triangle to be longer than the hypotenuse. This behavior occurs because, in spherical geometry, the concept of "side lengths" is based on angular separation along the surface of the sphere, rather than straight-line distances as in Euclidean geometry.
In fact as we show below, it is possible to draw a triangle with two 90° angles, and therefore two hypotenuses and still have the third leg larger than both of them.